Pythagorova Věta - Matematika

Pythagorova věta pochází od řeckého matematika Pythagorase už v 6. století př. n. l. Jde o vzorec, který umožňuje vypočítat všechny strany pravoúhlého trojúhelníku na základě 2 stran.

c2 = a2 + b2

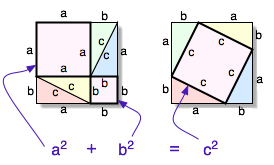a a b jsou odvěsny a c předpona troúhelníku.





Proč tam ale jsou a,b,c na druhou? Pythagoras se nad tím zamyslel a přišel na to, že obsah čtverce nad odvěsnami se rovná obsahu čtverce nad přeponou. Těžko si to lze představit. Ukážeme si to na příkladu:

Máme trojúhelník, kde je strana a = 3 cm, strana b = 4 cm, strana c = 5 cm. Funguje to tak, že když si uděláme z každé strany čtverec a vypočítáme obsah, tak součet obsahů a a b se musí rovnat obsahu c.


Takže,
obsah čtverce A se stranou a=3cm. Obsah by se rovnal 9 cm2
obsah čtverce B se stranou b=4cm. Obsah by se rovnal 16 cm2
Kdybychom znali pouze stranu a a b, snadno bychom vypočítali stranu c podle Pythagorova vzorce.

c2 = 9 + 16
c = odmocnina (25)
c = 5

Podíváme se na znovu na příklad a výsledek souhlasí.
Úloha: [ 1 ]  [ 2 ]  [ 3 ]  

Zadání:

Vypočítejte v pravoúhlém trojúhelníku stranu a, když je strana b=3cm a strana c=4cm. Pravý úhel je u vrcholu A.

Řešení

Zadání:

Vypočítejte v pravoúhlém trojúhelníku stranu c, když je strana a=3cm a strana b=8cm. Pravý úhel je u vrcholu B.

Řešení

Zadání:

Vypočítejte tělěsovou úhlopříčku v kvádru, když je strana a=7cm, strana b=5cm a výška v=4cm.

Řešení

Překlad z a do vietnamštiny | Online překladač